山頂の気温が低いのは、気圧が低いためです。標高が100m高くなるたびに気圧は約10hPa下がり、気温は約0.6℃下がるといわれています。これと同じことが海洋でも起こります。
深層になるほど海水は圧力の影響を強く受け、わずかですが水温が高めに出ます。したがって海水の密度を考えるとき、圧力を一定にして考える必要があります。このため気象学でいうところの温位に相当するものとして、海洋学にはポテンシャル水温というものがあります。
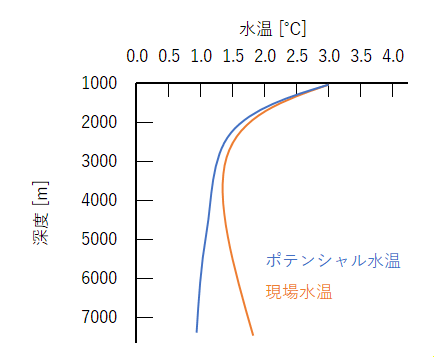
ポテンシャル水温とは、海水を断熱的(周囲と熱のやり取りなし)にある基準の深さまで持ってきたとき、その海水の示す水温を表します。これに対して、その場所での水温を現場水温といいます。通常基準の深さは海面にとります。またポテンシャル水温と塩分から計算した密度を、ポテンシャル密度といいます。
ポテンシャル水温の計算式
- 本計算式の定義は古く、現在の温度の定義ITS-90とは異なるIPTS-68の時代のものです。このため本計算を行うためには、ITS-90とIPTS-68の温度換算が必要です。本ページ内において「$T$」はITS-90の温度を、「$t$」はIPTS-68の温度を表します。
- 1MPa = 100dbar ≒ 100m

実用塩分を$S$、現場水温を$T$ [℃]、現場圧力を$P$ [dbar]、基準圧力を$P_{r}$ [dbar]とすると、ポテンシャル水温$\theta$ [℃]は下記式1により求められます。なおポテンシャル水温の計算は少し特殊で、下記式を上から順に計算していくことになります。
$ \begin{aligned}
t &= 1.00024 \cdot T \\
h &= P_{r} – P \\
xk &= h \cdot {\rm \Gamma}(S, t, P) \\
t &= t + 0.5 \cdot xk \\
q &= xk \\
p &= P + 0.5 \cdot h \\
xk &= h \cdot {\rm \Gamma}(S, t, p) \\
t &= t + 0.29289322 \cdot (xk – q) \\
q &= 0.58578644 \cdot xk + 0.121320344 \cdot q \\
xk &= h \cdot {\rm \Gamma}(S, t, p) \\
t &= t + 1.707106781 \cdot ( xk – q ) \\
q &= 3.414213562 \cdot xk – 4.121320344 \cdot q \\
p &= p + 0.5 \cdot h \\
xk &= h \cdot {\rm \Gamma}(S, t, p) \\
\theta’ &= t + \frac{ xk – 2.0 \cdot q }{ 6.0 }\\
\theta(S, T, P, P_{r}) &= \theta’ \cdot 0.99976
\end{aligned} $
ここで${\rm \Gamma}(S, t, p)$は下記式により求められます。
$ \begin{aligned}
{\rm \Gamma}(S, t, p) &= a_{0} + a_{1} \cdot t + a_{2} \cdot t^{2} + a_{3} \cdot t^{3} + \left( b_{0} + b_{1} \cdot t \right) \cdot ( S – 35 ) \\
& + \left\{ c_{0} + c_{1} \cdot t + c_{2} \cdot t^{2} + c_{3} \cdot t^{3} +
\left( d_{0} + d_{1} \cdot t \right) \cdot ( S – 35 ) \right\} \cdot p \\
& + \left( e_{0} + e_{1} \cdot t + e_{2} \cdot t^{2} \right) \cdot p^{2}
\end{aligned} $
なお上記計算式で使用する係数は下記のとおりです。
$a_{0} = 3.5803 \times 10^{-5}$、$a_{1} = 8.5258 \times 10^{-6}$、$a_{2} = -6.8360 \times 10^{-8}$、$a_{3} = 6.6228 \times 10^{-10}$
$b_{0} = 1.8932 \times 10^{-6}$、$b_{1} = -4.2393 \times 10^{-8}$
$c_{0} = 1.8741 \times 10^{-8}$、$c_{1} = -6.7795 \times 10^{-10}$、$c_{2} = 8.7330 \times 10^{-12}$、$c_{3} = -5.4481 \times 10^{-14}$
$d_{0} = -1.1351 \times 10^{-10}$、$d_{1} = 2.7759 \times 10^{-12}$
$e_{0} = -4.6206 \times 10^{-13}$、$e_{1} = 1.8676 \times 10^{-14}$、$e_{2} = -2.1687 \times 10^{-16}$
| $S$ | $t$ [℃] | $P$ [dbar] | $P_r$ [dbar] | $\theta’$ [℃] |
|---|---|---|---|---|
| 25 | 10 | 1000 | 0 | 9.8935 |
| 30 | 20 | 5000 | 0 | 19.0211 |
| 35 | 30 | 10000 | 0 | 27.3851 |
サンプルコード
[potential_temp.c]
/**
* @file potential_temp.c
* @brief ポテンシャル水温の計算
* @brief 1MPa = 100dbar
*/
//------------------------------------------------------------------------------
// include
//------------------------------------------------------------------------------
#include "potential_temp.h"
//------------------------------------------------------------------------------
// private function
//------------------------------------------------------------------------------
static double Calc_ATG(double sal, double temp, double press);
/** ----------------------------------------------------------------------------
* @brief ポテンシャル水温の計算
* @details UNESCO (1983) "Potential Temperature"
*
* @param temp : 現場水温[℃] (ITS-90)
* @param sal : 塩分
* @param press : 現場圧力[dbar]
* @param press0 : 基準圧力[dbar]
* @return ポテンシャル水温[℃] (ITS-90)
*/
double Calc_PotentialTemp(double temp, double sal, double press, double press0)
{
double h, p, q, t, xk;
double ptemp;
t = temp * 1.00024; // ITS-90 ⇒ IPTS-68
h = press0 - press;
xk = h * Calc_ATG(sal, temp, press);
t = t + 0.5 * xk;
q = xk;
p = press + 0.5 * h;
xk = h * Calc_ATG(sal, t, p);
t = t + 0.29289322 * (xk - q);
q = 0.58578644 * xk + 0.121320344 * q;
xk = h * Calc_ATG(sal, t, p);
t = t + 1.707106781 * (xk - q);
q = 3.414213562 * xk - 4.121320344 * q;
p = p + 0.5 * h;
xk = h * Calc_ATG(sal, t, p);
ptemp = t + (xk - 2.0 * q) / 6.0;
ptemp *= 0.99976; // IPTS-68 ⇒ ITS-90
return ptemp;
}
/** ----------------------------------------------------------------------------
* @brief 断熱温度勾配 (Adiabatic Temperature Gradient)
*
* @param sal : 塩分
* @param temp : 温度[℃]
* @param press : 圧力[dbar]
* @return 断熱温度勾配[℃/dbar]
*/
static double Calc_ATG(double sal, double temp, double press)
{
static const double a[4] = {3.5803e-5, 8.5258e-6, -6.8360e-8, 6.6228e-10};
static const double b[2] = {1.8932e-6, -4.2393e-8};
static const double c[4] = {1.8741e-8, -6.7795e-10, 8.7330e-12, -5.4481e-14};
static const double d[2] = {-1.1351e-10, 2.7759e-12};
static const double e[3] = {-4.6206e-13, 1.8676e-14, -2.1687e-16};
double gamma, ds;
double t, t2, t3;
double aa, bb, cc, dd, ee;
t = temp;
t2 = t * t;
t3 = t2 * t;
aa = a[0] + a[1] * t + a[2] * t2 + a[3] * t3;
bb = b[0] + b[1] * t;
cc = c[0] + c[1] * t + c[2] * t2 + c[3] * t3;
dd = d[0] + d[1] * t;
ee = e[0] + e[1] * t + e[2] * t2;
ds = sal - 35.0;
gamma = aa + bb * ds + (cc + dd * ds) * press + ee * press * press;
return gamma;
}[potential_temp.h]
#ifndef POTENTIAL_TEMP_H
#define POTENTIAL_TEMP_H
#ifdef __cplusplus
extern "C" {
#endif
//------------------------------------------------------------------------------
// function
//------------------------------------------------------------------------------
double Calc_PotentialTemp(double temp, double sal, double press, double press0);
#ifdef __cplusplus
}
#endif
#endifサンプルコードの使用例
使用例代わりに、CppUTestによるテストコードを掲載しておきます。
#include "CppUTest/TestHarness.h"
#include "potential_temp.h"
// clang-format off
TEST_GROUP(ptemp){
TEST_SETUP(){
}
TEST_TEARDOWN(){
}
};
// clang-format on
TEST(ptemp, Test_ptem)
{
double ptemp;
ptemp = Calc_PotentialTemp(10.0 / 1.00024, 25.0, 1000.0, 0.0);
DOUBLES_EQUAL(ptemp, 9.8935 * 0.99976, 5e-5);
ptemp = Calc_PotentialTemp(20.0 / 1.00024, 30.0, 5000.0, 0.0);
DOUBLES_EQUAL(ptemp, 19.0211 * 0.99976, 5e-5);
ptemp = Calc_PotentialTemp(30.0 / 1.00024, 35.0, 10000.0, 0.0);
DOUBLES_EQUAL(ptemp, 27.3851 * 0.99976, 5e-5);
}
脚注
- UNESCO (1983) “Potential Temperature” Unesco technical papers in marine science No.44 ↩︎

コメント