浮動小数点数は誤差に気を付けること | C言語

2023-10-142024-06-29

コンピューターは小数の取り扱いが苦手です。整数演算と違い複雑な処理を内部で行っています。しかし日常使用で気を付けることはそう多くありません。演算のたびに誤差が積み重なる点にだけ気をつけておけば良いでしょう。

フォーマット（IEEE 754）

C言語では浮動小数点数の扱いについて規定されていませんが、ほとんどの処理系では浮動小数点数のフォーマットにIEEE 754を採用しています。このフォーマットでは、浮動小数点数を下図のように扱います。

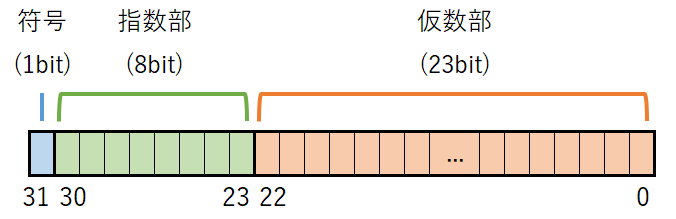
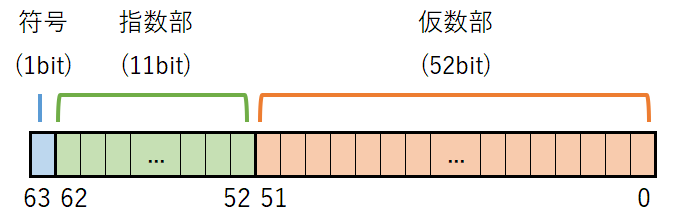
上図の符号(S)、指数部(E)、仮数部(F)から、浮動小数点数は下記式により数値に計算します。

単精度：$(-1)^S\left(1+\displaystyle\sum_{i=1}^{23}F_{-i}2^{-i}\right)\times2^{E-127}$

倍精度：$(-1)^S\left(1+\displaystyle\sum_{i=1}^{52}F_{-i}2^{-i}\right)\times2^{E-1023}$

ここで注目すべきは「1+」で、仮数部の最上位ビットが1となるように正規化しています。これにより単精度であれば、23ビット枠で24ビット分の数値を表すことができます。しかしすべての数値を上記正規化数で表しているわけではなく、次項に示す特殊表現があります。

一般的にfloat型は単精度、double型は倍精度ですが、処理系によっては単精度のdouble型も存在します。型のサイズ規定は「float≦double」です。初めて使用する処理系では、<float.h>などで型のサイズを確認してください。

IEEE 754にも1985、2008、2019などいくつかのバージョンがあります。このうちC言語の処理系で一般的に対応しているのは、IEEE 754-1985です。なお次期C言語の規格（C2x）では、2008年版または2019年版へ対応される計画です。
上記以外にも16ビットの半精度と、128ビットの四倍精度があります。しかしC言語では対応していないため詳細は述べません。なお半精度ですが、これは精度を犠牲にしてでも高速で処理したい用途に使用します。CPUの性能が低い場合に使用されるわけではありません。

特殊表現

IEEE 754では、先に示した正規化数以外に、次に示す特殊表現があります。

スクロールできます

符号	指数部	仮数部	内容
0	0	0	+0
1	0	0	-0
x	0	0以外	非正規化数（アンダーフロー）
0	255	0	+∞
1	255	0	-∞
x	255	222 以上	非数（quiet NaN）
x	255	222 > 仮数部 > 0	非数（signaling NaN）

単精度の特殊表現

スクロールできます

符号	指数部	仮数部	内容
0	0	0	+0
1	0	0	-0
x	0	0以外	非正規化数（アンダーフロー）
0	2047	0	+∞
1	2047	0	-∞
x	2047	251 以上	非数（quiet NaN）
x	2047	251 > 仮数部 > 0	非数（signaling NaN）

倍精度の特殊表現

「+0」と「-0」は同値です。if文で判定するとイコールとなります。
∞同士を比較すると一致しますが、NaN同士を比較しても不一致となります。
「signaling NaN」はNaN検出時に例外信号を出し、これによりOSが例外を発報します。
「quiet NaN」は、NaNを検出しても例外信号を出しません。
NaN検出時に「signaling」と「quiet」のどちらになるかは、プログラミング言語や処理系に依存します。

最小値・最大値

いわゆるFLT_MINやFLT_MAXは下記値になります。

スクロールできます

	最小値	最大値
単精度	2^-126 ≒ 1.17549435e^-38	2¹²⁷ ≒ 3.402823466e⁺³⁸
倍精度	2^-1022 ≒ 2.2250738585072014e^-308	2¹⁰²³ ≒ 1.7976931348623157e⁺³⁰⁸

なおここでいう最小値と最大値は下記の意味となります。

最小値：正規化数で表現できる最小の正の数。
最大値：正規化数で表現できる最大の正の数。

非正規化数

正規化数で表せる最小値は、単精度の場合で1.17549435e^-38です。このままでは、-1.17549435e^-38～+1.17549435e^-38の間の演算結果はすべてゼロになってしまいます。そこでゼロ近辺をもっと細かく表現しようとしたのが非正規化数で、下記のように計算します。

単精度：$(-1)^S\left(0+\displaystyle\sum_{i=1}^{23}F_{-i}2^{-i}\right)\times2^{-126}$

倍精度：$(-1)^S\left(0+\displaystyle\sum_{i=1}^{52}F_{-i}2^{-i}\right)\times2^{-1022}$

非正規化数では小数点の位置は固定となります。このためゼロに近づくほど有効数字が小さくなり、誤差が大きくなります。

有効数字

正規化数の有効数字は、仮数部のビット数で決まります。

単精度：2²³ ＝ 8388608 ⇒ 有効数字6桁
倍精度：2⁵² ≒ 4.5036e+15 ⇒ 有効数字15桁

有効桁数は、<float.h>で定義された「FLT_DIG」や「DBL_DIG」で取得できます。

浮動小数点数の誤差

コンピューターで表せられる数には限界があり、演算を行うたびに誤差が積み重なっていきます。演算結果の誤差には次のものがあります。

オーバーフロー: 演算結果の絶対値が最大値を超えるとオーバーフローとなります。
アンダーフロー: 演算結果の絶対値が最小値を下回るとアンダーフローとなります。アンダーフローはまず非正規化数となり、さらに進むと0となります。
丸め誤差: 仮数部の桁数を超えると、その桁数に収まるように四捨五入して丸められます。
例：x / 5.0 ≒ x * 0.2 、 x + x * y ≒ x * (1.0 + y)
打ち切り誤差: 無限級数など無限に続く計算はどこかで打ち切る必要があります。これにより発生する誤差が打ち切り誤差です。
情報落ち: 絶対値の大きい数と絶対値の小さい数を加減算したとき、絶対値の小さい数が無視されてしまう現象です。浮動小数点数の演算では指数を揃えます。このとき絶対値の小さい値が分解能を下回ると、ゼロになってしまいます。
例：分解能が4桁とすると…
　　1.234×10²+1.0×10^-2 = 1.234×10²+0.0001×10² ≒ 1.234×10²+0
桁落ち: 値がほぼ等しい数同士の減算を行ったとき、有効数字が減少すること。
例：有効数字が4桁とすると、下記の計算の結果有効数字は2桁に減少します。
　　1.333… – 1.321… ≒ 1.333 – 1.321 = 0.012

浮動小数点数の比較

浮動小数点数の演算には丸め誤差が発生します。例えば「0.1」と「1.0 – 0.9」は等価とはなりません。このため浮動小数点数の比較は、誤差を考慮して行う必要があります。

#include <float.h>
#include <math.h>

double d1 = 0.1;
double d2 = 1.0 - 0.9;

// 十分に近い値なら一致とみなす
if (fabs(d1 - d2) <= DBL_EPSILON) {
  ...
}

上記「DBL_EPSILON」は<float.h>で定義された計算機イプシロンで、「1より大きい最小の数」と「1」との差です。ただし計算機イプシロンは1が基準のため、扱う値が大きい場合は値に合わせた比を考える必要があります。このため比較は次のように行うといいでしょう。

#include <float.h>
#include <math.h>

double d1, d2;
double eps;

// "1, d1, d2"の中で一番大きい値をイプシロンに掛ける
eps = DBL_EPSILON * fmax(1, fmax(fabs(d1), fabs(d2)));

// d1 = d2 ?
if (fabs(d1 - d2) <= eps) {
  ...
}

// d1 > d2 ?
if (d1 > (d2 + eps)) {
  ...
}

// d1 >= d2 ?
if ((d1 + eps) > d2) {
  ...
}

また上記例は次のようにまとめることもできます。

#include <float.h>
#include <math.h>

int fpncmp(double d1, double d2) {
  double eps = DBL_EPSILON * fmax(1, fmax(fabs(d1), fabs(d2)));

  if (d1 > (d2 + eps)) {
    return 1;
  } else if (d2 > (d1 + eps)) {
    return -1;
  } else {
    return 0;
  }
}

// 使用例
if (fpncmp(d1, d2) > 0)   // d1 > d2
if (fpncmp(d1, d2) >= 0)  // d1 >= d2
if (fpncmp(d1, d2) == 0)  // d1 == d2
if (fpncmp(d1, d2) <= 0)  // d1 <= d2
if (fpncmp(d1, d2) < 0)   // d1 < d2